Двойной интеграл.

 

Понятие двойного интеграла.

 

Примеры решения двойных интегралов.

 

Геометрический смысл двойного интеграла.

---

Понятие двойного интеграла

Примеры решения двойных интегралов

Двойной интеграл - это обобщение определенного интеграла на двумерный случай. Т.е. для определения понятия двойного интеграла используется функция, зависящая уже от двух переменных: f(x,y). Эта функция должна быть определена на некоторой, обладающей конечной площадью, области D плоскости X0Y. При этом граница области D должна состоять из конечного числа графиков непрерывных функций.          Не трогать

Обозначение двойного интеграла

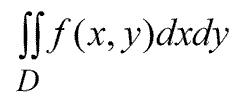
Геометрический смысл двойного интеграла.

Перейти к примерам решения двойных интегралов.

Для того, чтобы понять, что же представляет из себя двойной интеграл с геометрической точки зрения, давайте посмотрим на рисунок ниже.

Итак, пусть в пространстве мы имеем некоторое тело (криволинейный цилиндр [в отличие от криволинейной трапеции в определенном интеграле]), ограниченное сверху поверхностью f(x,y), по бокам - некоторой цилиндрической поверхностью (образующие которой параллельны оси OZ), а снизу плоскостью X0Y.

Не углубляясь особо в теорию, возьмем из нее главное: Геометрический смысл двойного интеграла: при неотрицательной функции f(x,y), двойной интеграл по области D представляет из себя объем криволинейного цилиндра, который построен на области D и ограничен сверху поверхностью z=f(x,y).

Метки страницы: Понятие двойного интеграла; Обозначение двойного интеграла; Геометрический смысл двойного интеграла.