Решение производных онлайн.
Найти производную онлайн.
Вычисление производных онлайн.
На данной странице Вы можете произвести решение производных онлайн. В результате Вы получите развернутое решение производной с комментариями о ходе решения. В развернутом решении производной будет содержаться первая и вторая производные Вашей функции.
То есть, чтобы найти производную функции, нужно ввести функцию в калькуляторе производных, который расположен ниже и нажать на кнопку: "Найти производную". Затем, вы получите решение в режиме online.
Наряду с решением производной в режиме онлайн, Вы можете заказать у нас «ручное» вычисление производных через форму заказа. Кроме этого, Вы можете вычислить производную самостоятельно с помощью таблицы производных функций.
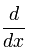 |
Сюда не жать |
| ШТРИХ вводить НЕ нужно. Только функцию. |
| ПРАВИЛЬНЫЙ синтаксис ввода функций описан ниже. |
| Примеры: | |
| Аргумент функции пишется в квадратных скобках: [x] | Например: sin[ln[x]], sin[ln[x]]^cos[x], sin[x], cos[2x] |
Икс делить на два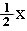 | x/2 либо 0.5x либо (1/2)x |
Единица делить на икс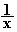 | 1/x |
| Квадратный корень из икс | sqrt[x] |
Корень третьей степени 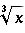 | x^(1/3) |
Умножение двух функций (сложная функция) | (x*sin[x])^(2x) т.е. используем значок * |
Степень числа: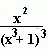 | Например: x^2/(1+x^3)^3, (x+8)^3, e^(x+1) |
| Натуральный логарифм | ln[x] |
Сложная функция, пример  | sin[2*ln[x]] |
Сложная функция, пример 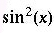 | sin^2[x] |
Обратные тригонометрические функции, пример 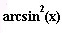 | arcsin^2[x] |
Дробно-рациональная функция, пример  | (x^2-3x+5)/((x+1)(x-2)(x+2)^2) |
